The last problem seemed pretty straightforward, but now consider the following scenario
The work for this problem is very similar to the last, and we find the second key with a series of XORs. The code should make this clear if you need a hint ;)
Source of this and previous question: Stanford Crypto Class HW from winter 2010 (problem #2).
given 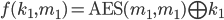 and
and 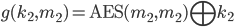 , find
corresponding
, find
corresponding 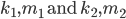 such that a collision between the functions occurs.
such that a collision between the functions occurs.
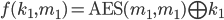 and
and 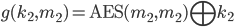 , find
corresponding
, find
corresponding 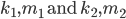 such that a collision between the functions occurs.
such that a collision between the functions occurs.
The work for this problem is very similar to the last, and we find the second key with a series of XORs. The code should make this clear if you need a hint ;)
from Crypto.Cipher import AES
from Crypto.Util.strxor import strxor as xor
from Crypto import Random
from binascii import hexlify as hexify
# find a, b, x, and y such that
# AES(x, x) XOR y == AES(a, a) XOR b
# Note that for clarity, these names are not used
# each variable is referred to as a m (message) or a k(key)
# and AES takes arguments (key, message)
def collision2():
random = Random.new()
m1 = random.read(16)
k1 = random.read(16)
m2 = random.read(16)
key1 = AES.new(m1, AES.MODE_ECB)
key2 = AES.new(m2, AES.MODE_ECB)
f = xor(key1.encrypt(m1), k1)
k2 = xor(xor(key1.encrypt(m1), key2.encrypt(m2)), k1)
g = xor(key2.encrypt(m2), k2)
print("f: %s\ng: %s" %(hexify(f), hexify(g)))
if __name__ == '__main__':
collision2()
Source of this and previous question: Stanford Crypto Class HW from winter 2010 (problem #2).
Cryptography
Python